Yörüngesel Zarafet Gezegenlerin Zarif Dansı

Gök cisimleri birbirlerinin çevresinde zarif yörüngelerde hareket ederler. Bu yörüngelerin zarif eğrileri fizik yasalarının bir sonucudur.

Bu makalede, gök cisimlerinin zarif hareketlerini inceleyeceğiz. Bu hareketleri tanımlayan mahrek elemanlarını, Kepler’in gezegensel hareket yasalarını, Newton’un kütle çekim yasasını ve evrensel kütle çekim yasasını tartışacağız. Ek olarak kaçış hızını, Hohmann aktarma yörüngesini, jeostasyon yörüngelerini ve Lagrangian noktalarını da tartışacağız.

Bu yazının sonucunda gök cisimlerinin zarif hareketlerini ve bu tarz şeyleri yöneten fiziği daha iyi anlayacaksınız.

Hususiyet	Tarif
Gök cisimleri	Bir yıldızın çevresinde dönen gezegenler, uydular, asteroitler ve kuyrukluyıldızlar benzer biçimde uzaydaki nesneler.
Zarafet	Gök cisimlerinin hareketlerindeki zarafet yahut güzellik.
Mahrek mekaniği	Gezegenler, uydular, asteroitler ve kuyrukluyıldızlar benzer biçimde uzaydaki cisimlerin hareketlerini inceleyen bilim dalı.
Gezegensel hareket	Gezegenlerin bir star etrafındaki hareketi.
Feza bilimi	Uzayı ve gezegenler, uydular, asteroitler, kuyrukluyıldızlar, yıldızlar, galaksiler ve kainat benzer biçimde uzaydaki nesneleri inceleyen bilim dalı.

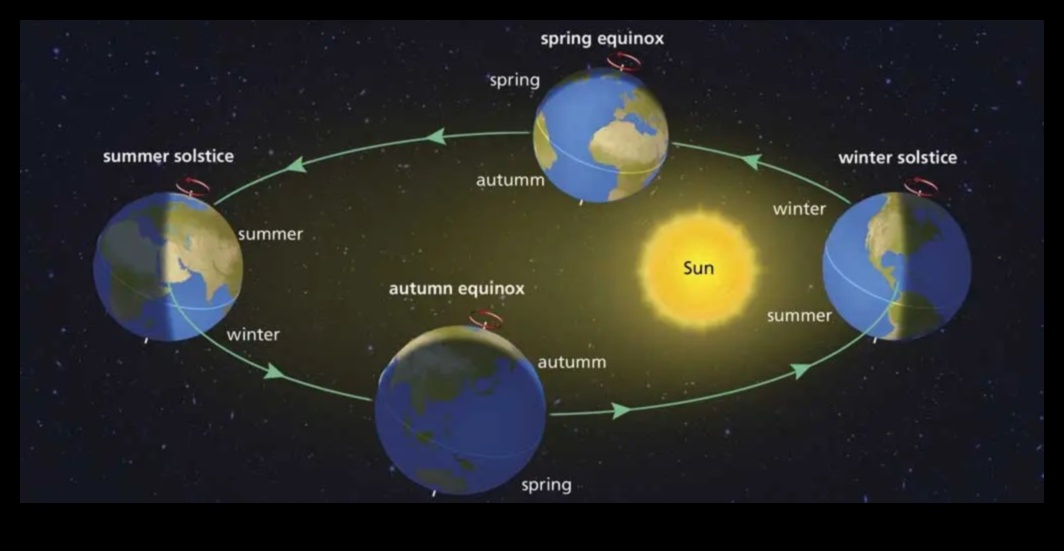
II. Yörüngesel Elemanlar

Mahrek elemanları, bir yörüngenin şeklini ve yönelimini tanımlayan parametrelerdir. Gök cisimlerinin hareketini takip etmek ve gelecekteki konumlarını kestirmek için kullanılırlar. En yaygın mahrek elemanları şunlardır:

• Yarı büyük eksen (a): Mahrek merkezinden odağa olan uzaklık.
• Eksantriklik (e): Yörüngenin ne kadar eliptik bulunduğunun bir ölçüsü.
• Eğim (i): Mahrek düzlemi ile referans düzlemi arasındaki açı.
• Yükselen düğümün boylamı (Ω): Yörüngenin referans düzlemini güneyden kuzeye kestiği nokta ile referans yönünden olan açı.
• Periapsis argümanı (ω): Yükselen düğümden yörüngenin merkezi gövdeye en yakın olduğu noktaya kadar olan açı.
• Yaklaşık anomali (M): Yörüngedeki cismin periapsisden açısal uzaklığı, aşama olarak ölçülür.

Bu elemanlar, Dünya ve Ay benzer biçimde iki gövdeli bir sistemdeki bir cismin yörüngesini tarif etmek için yeterlidir. Sadece, gezegenler ve Güneş benzer biçimde daha karmaşa sistemlerdeki cisimlerin yörüngelerini tarif etmek için ek elemanlara gereksinim vardır.

Kepler’in Gezegen Hareketi Yasaları

Kepler’in gezegen hareketi yasaları gezegenlerin Güneş etrafındaki hareketini tanımlar. ilk başlarda Johannes Kepler tarafınca 1609’da yayınlanmış olup, onun uzun seneler süresince gezegenler üstünde meydana getirdiği gözlemlere dayanmaktadır.

Birinci yasa, gezegenlerin eliptik yörüngelerde hareket ettiğini ve Güneş’in elipsin bir odağında bulunduğunu belirtir. İkinci yasa, bir gezegenin hızının Güneş’e en yakın olduğunda en yüksek, Güneş’ten en uzak olduğunda ise en yavaş bulunduğunu belirtir. Üçüncü yasa, bir gezegenin mahrek sürecinin karesinin, yörüngesinin yarı büyük ekseninin küpüne orantılı bulunduğunu belirtir.

Kepler’in gezegen hareketi yasaları, güneş sistemini anlamamızın temel bir parçasıdır. Gezegenlerin, kuyrukluyıldızların ve asteroitlerin hareketlerini kestirmek için kullanılmışlardır ve ek olarak öteki gezegen sistemlerinin modellerini geliştirmek için de kullanılmıştır.

IV. Newton’un Yerçekimi Yasası

Newton’un kütle çekim yasası, iki nesne arasındaki kütle çekim kuvvetinin kütlelerinin çarpımıyla doğru orantılı ve aralarındaki mesafenin karesiyle ters orantılı bulunduğunu belirtir. Bu matematiksel olarak şöyle anlatım edilebilir:

Ç = Gm1m2/r^2

Burada F kütle çekim kuvveti, G kütle çekim sabiti, m1 ve m2 iki cismin kütleleri ve r aralarındaki mesafedir.

Newton’un kütle çekim yasası, fiziğin en temel yasalarından biridir ve gezegenlerin hareketinden gelgitlere kadar fazlaca muhtelif olguları açıklamak için kullanılır.

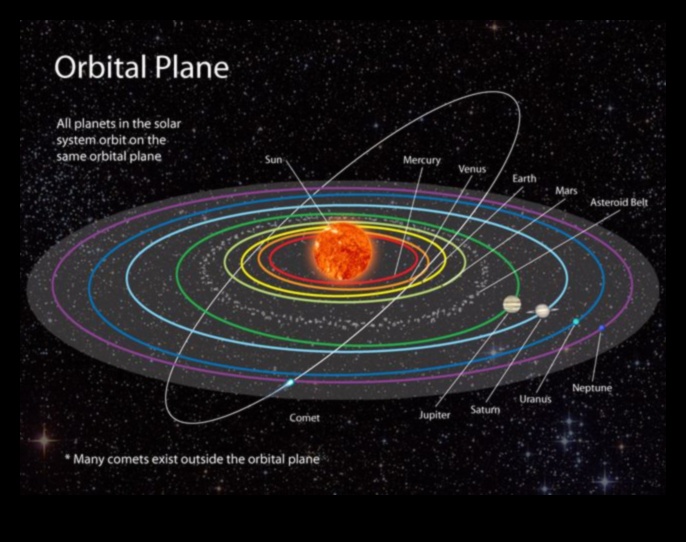
V. Evrensel Yerçekimi Yasası

Evrensel Yerçekimi Yasası, evrendeki her parçacığın öteki her parçacığı kütlelerinin çarpımıyla doğru orantılı ve aralarındaki mesafenin karesiyle ters orantılı bir kuvvetle çektiğini belirtir. Bu yasa İlk olarak 1687’de Isaac Newton tarafınca önerilmiştir ve fiziğin en temel yasalarından biridir.

Evrensel Çekim Yasası’nın denklemi şudur:

F = G * m1 * m2 / r^2

Neresi:

* F iki nesne arasındaki çekim kuvvetidir
* G yerçekimi sabitidir (6,674 × 10^-11 N m^2 kilo^-2)
* m1 ve m2 iki nesnenin kütleleridir
* r iki nesne arasındaki mesafedir

Evrensel Yerçekimi Yasası, gezegenlerin güneş etrafındaki hareketi, gelgitler ve kuyruklu yıldızların yörüngeleri benzer biçimde fazlaca muhtelif olguları açıklamak için kullanılabilen fazlaca kuvvetli bir yasadır. Ek olarak genel göreliliğin temel yasalarından biridir.

VI. Kaçış Hızı

Kaçış hızı, bir cismin bir gezegenin yahut öteki bir gök cisminin kütle çekim etkisinden kurtulabilmesi için ihtiyaç duyulan en düşük hızdır.

Kaçış hızı şu formülle bulunur:

v_Esc = √(2GM/dk)

Neresi:

• v_Esc kaçış hızı saniyede metre cinsindendir
• G yerçekimi sabitidir (6,674 × 10^-11 N·m²/kg²)
• M gezegenin yahut gök cisminin kütlesidir (kg cinsinden)
• r, gezegenin yahut gök cisminin merkezinden nesneye olan mesafedir (metre cinsinden)

Mesela Dünya yüzeyinden kaçış hızı saniyede ortalama 11,2 kilometredir.

Kaçış hızı feza seyahatinde mühim bir faktördür. Bir feza aracını yörüngeye fırlatmak için ilk olarak kaçış hızına yetişmesi icap eder. Yörüngeye girdikten sonrasında feza aracı herhangi bir itici güce gerek kalmadan irtifasını koruyabilir.

Kaçış hızı feza sondalarının tasarımında da bir faktördür. Öteki gezegenlere yahut uydulara yolculuk etmek suretiyle tasarlanan feza sondaları, ayrıldıkları gezegenin yahut uydunun kaçış hızına ulaşabilmelidir.

VII. Hohmann Geçirme Yörüngesi

Hohmann aktarma yörüngesi, bir feza aracının en az yakıt miktarıyla bir dairesel yörüngeden diğerine geçişine müsaade eden bir mahrek türüdür. Ismini, İlk olarak 1925’te tanımlayan Alman mühendis Walter Hohmann’dan almıştır.

Hohmann aktarma yörüngesi iki bölümden kaynaklanır: Feza aracını ilk dairesel yörüngeden ikinci dairesel yörüngenin zirve noktasına götürmüş olan eliptik mahrek ve feza aracını ikinci dairesel yörüngenin zirve noktasından ikinci dairesel yörüngeye götürmüş olan ikinci eliptik mahrek.

Bir Hohmann aktarma yörüngesi için toplam süre, iki dairesel yörüngenin iki mahrek sürecinin toplamına eşittir. Bir Hohmann aktarma yörüngesi için ihtiyaç duyulan yakıt, iki dairesel yörüngenin özgül mahrek enerjileri arasındaki farka eşittir.

Hohmann aktarma yörüngesi, bir feza aracını bir dairesel yörüngeden diğerine aktarma etmenin en bereketli yoludur. Sadece, aktarma yörüngesi için ihtiyaç duyulan süreyi beklemek olası olmayabileceği için devamlı en iyi seçenek değildir. Birtakım durumlarda, bieliptik aktarma yörüngesi benzer biçimde değişik bir mahrek türü kullanmak daha bereketli olabilir.

Jeostatik Yörüngeler

Jeostatik mahrek, bir uydunun yahut başka bir nesnenin Dünya’nın kendi ekseni çevresinde dönmesiyle aynı hızda Dünya çevresinde döndüğü bir yörüngedir. Bu, uydunun Dünya yüzeyindeki muayyen bir noktanın üstündeki gökyüzünde aynı konumda kalmış olduğu demektir. Jeostatik yörüngeler, muayyen bir alan üstünde durağan(durgun) bir konumu koruması ihtiyaç duyulan telekomünikasyon uyduları, hava durumu uyduları ve öteki uydular için kullanılır.

Jeostatik bir yörüngenin yüksekliği Dünya ekvatorunun ortalama 35.786 kilometre (22.236 mil) üzerindedir. Bu yükseklikte, bir uydunun mahrek dönemi tam olarak 24 saattir, Dünya’nın dönüş periyoduyla aynıdır.

Jeostatik yörüngeler çok kararlıdır ve bu yörüngelerdeki uydular yörüngelerinde herhangi bir ayarlama yapılmadan senelerce yerinde kalabilir. Bu, jeostatik yörüngeleri Dünya yüzeyindeki muayyen bir alanı devamlı kapsaması ihtiyaç duyulan uydular için ülkü hale getirir.

Jeostatik yörüngelerin dezavantajı, Dünya’nın fazlaca üstünde olmalarıdır, bu da bu yörüngelerdeki uyduların Dünya yüzeyinden daha düşük yörüngelerdeki uydulardan fazlaca daha uzakta olduğu demektir. Bu, jeostatik yörüngelerdeki uydularla komünikasyon oluşturmayı daha zor hale getirir ve ek olarak uyduları bu yörüngelere fırlatmayı daha zor hale getirir.

Zorluklara karşın, jeostatik yörüngeler çağıl telekomünikasyon ve hava durumu tahmin altyapısının mühim bir parçasıdır. Jeostatik uydular, Dünya yüzeyinin geniş alanlarının devamlı kapsamını sağlar ve uzun mesafelerde komünikasyon sinyallerini iletebilirler.

IX. Lagrangian Noktaları

Lagrangian noktaları (hem de librasyon noktaları olarak da bilinir) uzayda ufak bir nesnenin iki büyük nesnenin (Dünya ve Ay benzer biçimde) çevresinde yörüngede dönebildiği ve hiçbirine çekilmediği beş konumdur. Bu noktalara, İlk olarak 1772’de bu tarz şeyleri tanımlayan Joseph-Louis Lagrange’ın ismi verilmiştir.

Lagrangian noktaları iki büyük nesneyi birleştiren çizgi süresince yer alır ve ufak nesnenin yörüngesi çevresinde eşit aralıklarla bulunurlar. İlk Lagrangian noktası (L1) iki büyük nesnenin tam ortasında yer alır ve ikinci Lagrangian noktası (L2) yörüngenin karşı tarafında yer alır. Üçüncü Lagrangian noktası (L3) yörüngesinde ufak nesneden 60 aşama önde yer alır ve dördüncü Lagrangian noktası (L4) yörüngesinde ufak nesneden 60 aşama geride yer alır. Beşinci Lagrangian noktası (L5) yörüngesinde ufak nesneden 60 aşama önde, sadece büyük nesnenin karşı tarafında yer alır.

Lagrangian noktaları sabittir, doğrusu bu noktalardan birine yerleştirilen ufak bir nesne daha büyük nesnelerden herhangi birine çekilmeden orada kalacaktır. Bu, Lagrangian noktalarını feza teleskopları ve öteki uydular için ülkü konumlar haline getirir.

S1: Orbital zarafet nelerdir?

A1: Mahrek zarafeti, gök cisimlerinin hareketlerinin güzelliği ve simetrisidir. Çoğu zaman gezegenlerin balesi yahut yıldızların dansı olarak tanımlanır.

S2: Mahrek hareketinin yasaları nedir?

A2: Mahrek hareketinin yasaları, nesnelerin yörüngedeki hareketini tanımlayan bir takım matematiksel denklemdir. ilk başlarda 17. yüzyılda Johannes Kepler tarafınca önerildiler ve o zamandan beri gezegenlerin, uyduların ve kuyruklu yıldızların hareketlerini doğru bir halde kestirmek için kullanıldılar.

S3: Mahrek zarafetinin birtakım örnekleri nedir?

A3: Mahrek zarafetinin birtakım örnekleri şunlardır:

* Gezegenlerin Güneş etrafındaki yörüngeleri hemen hemen daireseldir.
* Ay’ın Dünya etrafındaki yörüngesi eliptiktir, sadece muhteşem bir daireye fazlaca yakındır.
* Kuyrukluyıldızların Güneş etrafındaki yörüngeleri çok eliptiktir ve onları Güneş’ten fazlaca uzaklara götürebilirler.